2 Linear Regression

A linear regression model predicts the target as a weighted sum of the feature inputs. The linearity of the learned relationship makes the interpretation easy. Linear regression models have long been used by statisticians, computer scientists and other people who tackle quantitative problems.

Linear models can be used to model the dependence of a regression target y on some features x. The learned relationships are linear and can be written for a single instance i as follows:

The predicted outcome of an instance is a weighted sum of its p features. The betas   represent the learned feature weights or coefficients. The first weight in the sum   is called the intercept and is not multiplied with a feature. The epsilon   is the error we still make, i.e. the difference between the prediction and the actual outcome. These errors are assumed to follow a Gaussian distribution, which means that we make errors in both negative and positive directions and make many small errors and few large errors.

Various methods can be used to estimate the optimal weight. The ordinary least squares method is usually used to find the weights that minimize the squared differences between the actual and the estimated outcomes:

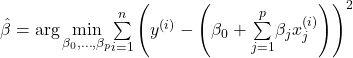
The biggest advantage of linear regression models is linearity: It makes the estimation procedure simple and, most importantly, these linear equations have an easy to understand interpretation on a modular level (i.e. the weights). This is one of the main reasons why the linear model and all similar models are so widespread in academic fields such as medicine, sociology, psychology, and many other quantitative research fields. For example, in the medical field, it is not only important to predict the clinical outcome of a patient, but also to quantify the influence of the drug and at the same time take sex, age, and other features into account in an interpretable way.

Estimated weights come with confidence intervals. A confidence interval is a range for the weight estimate that covers the “true” weight with a certain confidence. For example, a 95% confidence interval for a weight of 2 could range from 1 to 3. The interpretation of this interval would be: If we repeated the estimation 100 times with newly sampled data, the confidence interval would include the true weight in 95 out of 100 cases, given that the linear regression model is the correct model for the data.