Encoding of Categorical Features
Christoph Molnar
There are several ways to encode a categorical feature, and the choice influences the interpretation of the weights.
The standard in linear regression models is treatment coding, which is sufficient in most cases. Using different encodings boils down to creating different (design) matrices from a single column with the categorical feature. This section presents three different encodings, but there are many more. The example used has six instances and a categorical feature with three categories. For the first two instances, the feature takes category A; for instances three and four, category B; and for the last two instances, category C.
Treatment coding
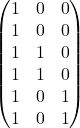
In treatment coding, the weight per category is the estimated difference in the prediction between the corresponding category and the reference category. The intercept of the linear model is the mean of the reference category (when all other features remain the same). The first column of the design matrix is the intercept, which is always 1. Column two indicates whether instance i is in category B, column three indicates whether it is in category C. There is no need for a column for category A, because then the linear equation would be overspecified and no unique solution for the weights can be found. It is sufficient to know that an instance is neither in category B or C.
Feature matrix:
Effect coding
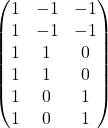
The weight per category is the estimated y-difference from the corresponding category to the overall mean (given all other features are zero or the reference category). The first column is used to estimate the intercept. The weight 
associated with the intercept represents the overall mean and 
, the weight for column two, is the difference between the overall mean and category B. The total effect of category B is 
. The interpretation for category C is equivalent. For the reference category A, 
is the difference to the overall mean and 
the overall effect.
Feature matrix:
Dummy coding
The 
per category is the estimated mean value of y for each category (given all other feature values are zero or the reference category). Note that the intercept has been omitted here so that a unique solution can be found for the linear model weights. Another way to mitigate this multicollinearity problem is to leave out one of the categories.
Feature matrix:
