Interpretation
Christoph Molnar
The interpretation of the weights in logistic regression differs from the interpretation of the weights in linear regression, since the outcome in logistic regression is a probability between 0 and 1. The weights do not influence the probability linearly any longer. The weighted sum is transformed by the logistic function to a probability. Therefore we need to reformulate the equation for the interpretation so that only the linear term is on the right side of the formula.
![]()
We call the term in the ln() function “odds” (probability of event divided by probability of no event) and wrapped in the logarithm it is called log odds.
This formula shows that the logistic regression model is a linear model for the log odds. Great! That does not sound helpful! With a little shuffling of the terms, you can figure out how the prediction changes when one of the features ![]() is changed by 1 unit. To do this, we can first apply the exp() function to both sides of the equation:
is changed by 1 unit. To do this, we can first apply the exp() function to both sides of the equation:
![]()
Then we compare what happens when we increase one of the feature values by 1. But instead of looking at the difference, we look at the ratio of the two predictions:
![]()
We apply the following rule:
![]()
And we remove many terms:
![]()
In the end, we have something as simple as exp() of a feature weight. A change in a feature by one unit changes the odds ratio (multiplicative) by a factor of ![]() . We could also interpret it this way: A change in
. We could also interpret it this way: A change in ![]() by one unit increases the log odds ratio by the value of the corresponding weight. Most people interpret the odds ratio because thinking about the ln() of something is known to be hard on the brain. Interpreting the odds ratio already requires some getting used to. For example, if you have odds of 2, it means that the probability for y=1 is twice as high as y=0. If you have a weight (= log odds ratio) of 0.7, then increasing the respective feature by one unit multiplies the odds by exp(0.7) (approximately 2) and the odds change to 4. But usually you do not deal with the odds and interpret the weights only as the odds ratios. Because for actually calculating the odds you would need to set a value for each feature, which only makes sense if you want to look at one specific instance of your dataset.
by one unit increases the log odds ratio by the value of the corresponding weight. Most people interpret the odds ratio because thinking about the ln() of something is known to be hard on the brain. Interpreting the odds ratio already requires some getting used to. For example, if you have odds of 2, it means that the probability for y=1 is twice as high as y=0. If you have a weight (= log odds ratio) of 0.7, then increasing the respective feature by one unit multiplies the odds by exp(0.7) (approximately 2) and the odds change to 4. But usually you do not deal with the odds and interpret the weights only as the odds ratios. Because for actually calculating the odds you would need to set a value for each feature, which only makes sense if you want to look at one specific instance of your dataset.
These are the interpretations for the logistic regression model with different feature types:
- Numerical feature: If you increase the value of feature
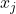 by one unit, the estimated odds change by a factor of
by one unit, the estimated odds change by a factor of 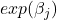
- Binary categorical feature: One of the two values of the feature is the reference category (in some languages, the one encoded in 0). Changing the feature
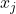 from the reference category to the other category changes the estimated odds by a factor of
from the reference category to the other category changes the estimated odds by a factor of 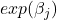
- Categorical feature with more than two categories: One solution to deal with multiple categories is one-hot-encoding, meaning that each category has its own column. You only need L-1 columns for a categorical feature with L categories, otherwise it is over-parameterized. The L-th category is then the reference category. You can use any other encoding that can be used in linear regression. The interpretation for each category then is equivalent to the interpretation of binary features.
- Intercept
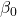 : When all numerical features are zero and the categorical features are at the reference category, the estimated odds are
: When all numerical features are zero and the categorical features are at the reference category, the estimated odds are 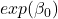
- The interpretation of the intercept weight is usually not relevant.

